Using Map-Reduce on Graphs

Map-Reduce seems to be the standard technology for working with large amounts of data these days. It is most well-known in combination with simple flat, table-like structures, maybe because most beginner tutorials focus on these.

However, using Map-Reduce, you can also do calculations on graphs. This is often done by employing message passing between the mapper and executing the map-reduce steps iteratively until some stop condition occurs. This can either be the length of the longest path in the graph (if known) or minimum a threshold the values must change for the iteration to continue.

The basic algorithm within the map and the reduce job is the same for many appliances. Might even be the same for all. In the mapper you first emit the node itself with it’s node id as the key. By emiting the node, you’ll be able to catch it in the reducer again. Then you iterate over all neighbouring nodes and calculate a message for each of them. You emit each neighbour’s node id together with this message.

def map(node, params):
    # check if we got result from a reducer (which also emits the key)
    if isinstance(node, tuple) or isinstance(node, list):
        node = node[1]

    yield node['id'], ('node', node)
    for adjacent_node in node['outgoing']:
        yield adjacent_node, ('msg', self.calc_message(node))

The reducer catches these messages and the node itself. It then uses both of them to calculate the new state for the node it just received. It can now emit the node with the new state and this output can be fed into the mapper again.

def reduce(rows_iter, out, params):
    from disco.util import kvgroup
    for node_id, passed_vals in kvgroup(rows_iter):
        node = None
        messages = []
        for type_id, val in passed_vals:
            if type_id == 'node':
                node = val
            elif type_id == 'msg':
                messages.append(val)


        # somebody is pointing to this node, but it does not exist
        if node == None:
            continue

        node['state'] = self.calc_state(node, messages)
        out.add(node_id, node)

Depending on the required appliance only the functions calc_message and calc_state have to be implemented. A quite simple example is the number of hops from one node in the graph to all other nodes. From the mapper you send a message to each neighbouring node with this node’s current distance plus one. In the reducer you check all messages a node received and take the minimum. Then you repeat from the beginning.

def calc_message(node):
    return node['state'] + 1

def calc_state(node, messages):
    if len(messages) == 0:
        return node['state']
    else:
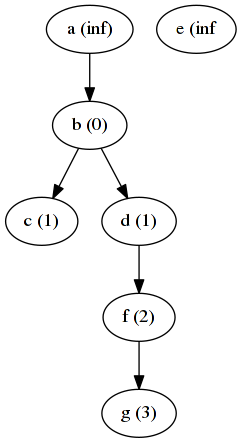
        return min(node['state'], min(messages))

For a simple example we start with a graph and define node b as the start node. This start node must be initialized to distance 0, while all other nodes are initialized to infinity.

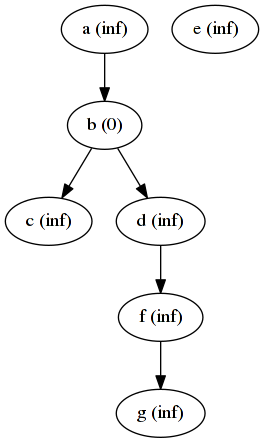
The algorithm then starts. In the first iteration, we will emit the old node distances (states) as seen on the first image, but we will also emit the distance of each node + 1 as a message to its neighbours. Let’s check this in more detail for nodes b and f.

When we get b as an input into our mapper, we will emit the node b itself first. Afterwards we iterate over c and d, because they are the outgoing nodes, and emit the message 1 to each of them (current distance of b plus one).

f has one outgoing edge to node g. Of course we also emit the node f itself followed by a message for node g with f’s distance plus one. However, f already has a distance of inifinity, so we will just send the message infinity to g.

In the reducer phase for d we will now collect its messages and calculate the minimum of d’s current distance and all incoming distances and assign this as the new distance for d. Since d has an own distance of inifinity and an incoming message with distance 1, we will assign distance 1 to it. e on the other hand has a distance of infinity and an incoming message of infinity, so we will just assign infinity again.

The resulting state after one iteration is as follows:

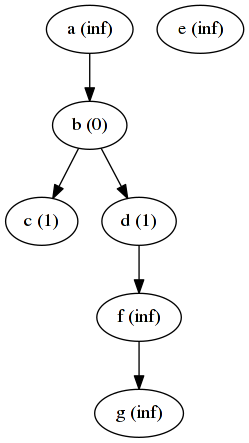
And the following two iterations will lead to these situations.

After 2 iterations:

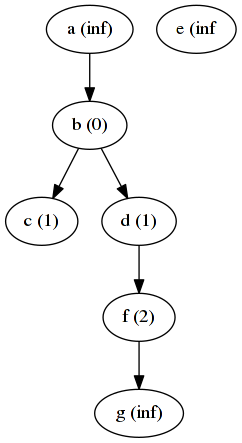
After 3 iterations: