Stein, Papier, Schere, Echse, Spock

Als Erweiterung von Schere, Stein, Papier gibt es zahllose Varianten. In meiner Kindheit waren Feuer und Wasser beliebt. Aus Big Bang Theory kennen wir die Variante “Stein, Papier, Schere, Echse, Spock” mit folgenden Regeln:

Schere schneidet Papier, Papier bedeckt Stein, Stein zerquetscht Echse, Echse vergiftet Spock. Spock zertrümmert Schere, Schere köpft Echse, Echse frisst Papier. Papier widerlegt Spock, Spock verdampft Stein. Und wie gewöhnlich – Stein schleift Schere.

Dies können wir in einem Graphen aufmalen, wobei ein Pfeil bedeutet, dass der Ursprung das Ziel schlägt.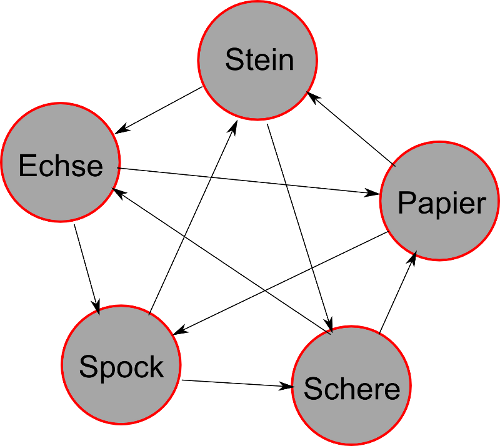

An diesem Graphen kann man schön sehen, dass das Spiel ausgeglichen ist. Außerdem existiert für jede Kombination (außer zwei gleichen Figuren) ein Spielausgang in Form von Sieg oder Niederlage.

Dies liegt daran, dass jede Figur aus dem Spiel im Graph exakt vier Kanten hat, wobei zwei Ausgangs- und zwei Eingangskanten sind.

Balanciertheit und Vollständigkeit

Formal können wir sagen, dass ein Spiel aus “Schere, Stein, Papier, …” genau dann ausgeglichen/balanciert ist, wenn gilt (wir nennen die Menge aller Spielfiguren S): \(\forall s \in S: d^{-}(s) = d^{+}(s)\)

Und es ist vollständig (=es existiert außer bei gleichen Figuren ein Ergebnis), wenn gilt: \(\forall s \in S: d(s) = S.length - 1\)

Das klassische Schere, Stein, Papier ist übrigens nur ein Subgraph des obigen Graphen.

Anzahl der Knoten muss ungerade sein

Was wir aus obiger Angabe auch sehen ist, dass ein solches Spiel nur vollständig und balanciert sein kann, wenn die Anzahl der Knoten ungerade ist.

1. Denn angenommen die Anzahl der Knoten ist gerade und das Spiel ist vollständig. Dann hat jeder Knoten S.length - 1 Kanten. Das ist aber eine ungerade Zahl. Zudem gilt immer \(d(s) = d^{-}(s) + d^{+}(s)\). Also kann die Bedingung \(d^{-}(s) = d^{+}(s)\) nicht gelten, denn dazu müsste d(s) gerade sein. Also ist das Spiel nicht balanciert.
2. Ist die Anzahl gerade und das Spiel ist hingegen balanciert. Dann gilt \(d^{-}(s) = d^{+}(s)\) für alle Knoten. Dann muss aber \(d(s) = d^{-}(s) + d^{+}(s)\) gerade sein, woraus folgt dass \(d(s) = S.length - 1\) nicht zutreffen kann (denn sowohl d(s) als auch S.length sind gerade).

Ich hätte erwartet, dass Spock bei Sheldons Spiel einen Vorteil hat. Allerdings vermute ich, dass unsere Feuer-Wasser-Variante auf dem Schulhof oft nicht ausgeglichen war, denn niemand wusste die Regeln so genau und es wurde immer ausdiskutiert, was logischer sei ;)