Algorithmen zur Bestimmung von Ähnlichkeiten

Zur Ermittlung der Ähnlichkeit zweier Mengen oder Messreihen gibt es verschiedene Algorithmen, die jedoch alle etwas unterschiedlich ablaufen und somit auch für unterschiedliche Zwecke besser oder schlechter geeignet sind.

Euklidischer Abstand

Der euklidische Abstand ist im Grunde eine sehr einfache Berechnung, die man aus der Schulzeit kennt. Damals wurde mit dem Satz des Pythagoras der Abstand zweier Punkte im zwei- und später auch im dreidimensionalen Raum ermittelt. Diesen Raum erweitert man nun einfach auf n Dimensionen, wobei n der Anzahl der verschiedenen Messdaten entspricht.

Der euklidische Abstand eignet sich allerdings nur, wenn Gleichheit nur durch gleiche Größen und nicht durch lineare Abhängigkeit bestimmt wird. Die Messdaten (1,2) sind nach dem euklidischen Abstand wesentlich anders als (2,4). Dies stellt sich als Problem heraus, wenn es nur um die relative Ähnlichkeit und nicht um absolute Werte geht (z.B. dass Wort A im Vergleich zu Wort B nur halb so oft vorkommt).

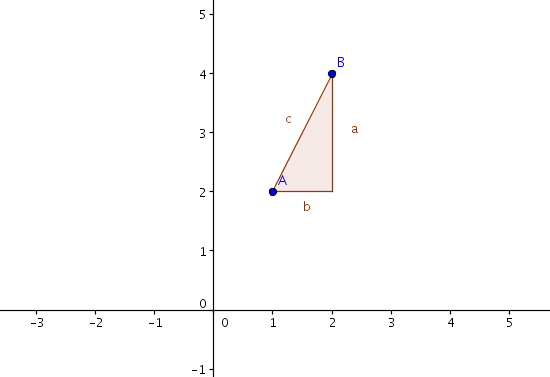
Will man dieses Problem beheben, müsste man mit Normalvektoren arbeiten. Dazu teilt man die einzelnen Vektoren durch ihren Betrag, womit jeder Vektor die Länge 1 erhält und es zu einer Verschiebung auf dem Einheitskreis kommt.

Tanimoto

Tanimoto hat den Jaccard-Index erweitert, sodass dieser auch mit nicht-binären Zahlen verwendet werden kann. Mit Jaccard ist es nur möglich, dass Werte entweder in der Menge vorhanden sind oder nicht (1 oder 0). Dank der Tanimoto-Formel können auch Werte wie 0,5 vorhanden sein.

Der Tanimoto-Koeffizient geht – ähnlich wie die Berechnung über den euklidischen Abstand – stark nach unten, wenn man zwei Reihen mit unterschiedlichen Werten, aber gleichem Verlauf miteinander vergleicht. Dafür schlägt Tanimoto weniger nach unten aus, wenn man einzelne Werte bei sehr stark korrelierenden Reihen verändert.

Pearson

Der Pearson-Korrelationskoeffizient verwendet eine Normalisierung und erkennt dadurch auch Korrelationen bei Vielfachen. So werden z.B. (4,6,8) und (8,12,16) vom Pearson-Korrelationskoffezienten als vollkommen korrelierend betrachtet.

Bildlich dargestellt ist der Pearson-Korrelationskoeffizient der Abstand aller Punktepaare aus beiden Vergleichsmengen in einem zweidimensionalen Koordinatensystem zu einer Regressionsgeraden. Liegen alle Punkte auf einer Geraden, ist der Koeffizient entweder +1 (bei positiver Steigung) oder -1 (bei negativer Steigung), wobei +1 eine vollkommene Korrelation und -1 eine negative Korrelation bedeutet.

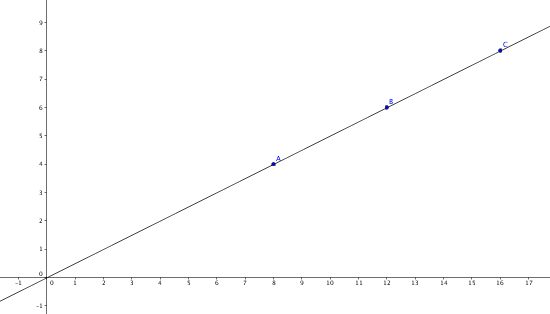
Der Pearson-Korrelationskoeffizient zeigt jedoch Schwächen bei Ausreißern, da diese die Regressionsgerade verschieben oder selbst einen sehr großen Abstand haben und damit den Koeffizienten verschlechtern. In meinem Testfall waren in zwei Reihen von jeweils fünf Werten vier Werte gleich und einer komplett anders, was bei Pearson zu einem Wert von nur noch 0,12 führte:

Kor((0.1 0.4 0.1 0.4 0.5), (0.1 0.4 0.7 0.4 0.5)) = 0.123278