Bloom- und Counting-Filter - probabilistische Datenstrukturen

Eine nützliche Datenstruktur, wenn man schnell ein Ergebnis braucht, ob etwas definitiv nicht vorhanden ist, sind Bloom-Filter. Sie sind eine probabilistische Datenstruktur, die falsch Positive aufweisen kann. Das bedeutet, dass die Antwort “X befindet sich in der Datenstruktur” nicht unbedingt richtig sein muss. Falsch Negative treten hingegen nicht auf, d.h. die Antwort “X befindet sich nicht in der Datenstruktur” ist immer richtig.

Bloom-Filter funktionieren mit einem Bitarray der Länge \(m\). Alle Stellen des Bitarrays sind zu Beginn auf 0 initialisiert. Über \(k\) verschiedene Hashfunktionen werden für einen Wert, der ins Bloom-Filter eingefügt werden soll, \(k\) Hashwerte berechnet. Diese geben die Stellen im Bitarray an, welche auf 1 gesetzt werden sollen.

Wird nun eine Abfrage gestellt, ob X sich im Bloom-Filter befindet, werden wieder alle Hashfunktionen auf X angewendet. Befindet sich dann an jeder der Stellen, die diese Hashfunktionen angeben, eine 0, so wurde X sicher nicht eingefügt. Befindet sich an mindestens einer Stelle eine 1, so wurde entweder X eingefügt oder die Stelle wurde doch ein anderes Element und dessen Hashwert auf 1 gesetzt.

Es lässt sich auch nicht sagen, dass ein Element sicher eingefügt wurde, wenn alle Stellen 1 sind. Schließlich könnten alle Stellen durch verschiedene andere Elemente auf 1 gesetzt worden sein. Deshalb ist die Datenstruktur bei positiven Rückmeldungen immer unsicher.

Aus einem Bloom-Filter können keine Elemente gelöscht werden. Dies könnte dazu führen, dass versehentlich Stellen auf 0 gesetzt werden, die zuvor von mehreren eingefügten Elementen auf 1 gesetzt worden waren. Da keine Zählung der Stellen vorgenommen wird, ist dies nicht zu erkennen. Das Bloom-Filter lässt sich jedoch sehr einfach zu einem Counting-Filter erweitern. Bei diesem werden Stellen beim Einfügen nicht auf 1 gesetzt, sondern um 1 inkrementiert. Beim Löschen werden diese Stellen dann um 1 dekrementiert, sodass bei mehreren Einfügeoperationen und einer Löschoperation auf derselben Stelle, die Stelle immer noch als belegt gilt. Der Speicherverbrauch steigt dadurch natürlich. Die Situation zu falsch Positiven und falsch Negativen bleibt die gleiche wie beim Bloom-Filter.

Beispiel

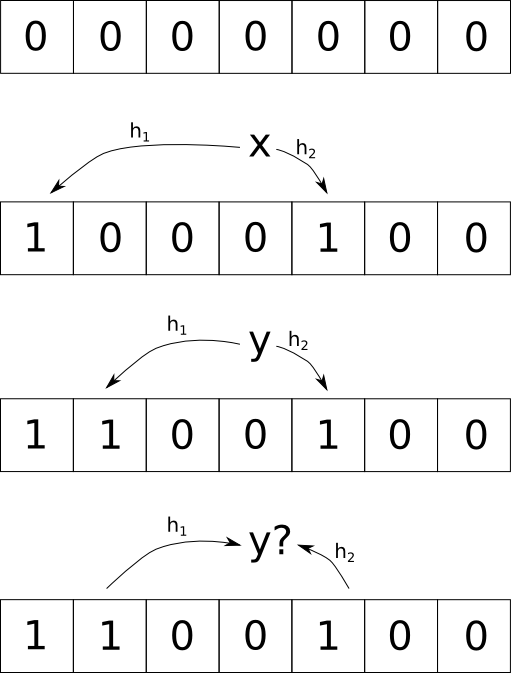
In folgendem Beispiel werden zunächst die Werte x und y in ein Bloom-Filter eingefügt. Diese werden durch zwei Hashfunktionen \(h_1\) und \(h_2\) in Stellen im Bitarray umgerechnet. Diese Stellen werden beim Einfügen jeweils auf 1 gesetzt. Anschließend wird geprüft, ob y im Bloom-Filter vorhanden ist.